If - in case of constant headways - the passenger makes use of the information on how long he has been waiting already at the stop, he will be able to reduce his expected remaining costs - in contrast to the previously described models. The passenger knows for example, that after waiting eight minutes, a line with 10 minutes headway has to arrive within the next two minutes. The passenger can make use of this information and ignore potentially earlier arriving lines, which are, however, at least two minutes slower.
The passenger has this information independently of the external infrastructure. To assume this is therefore not a strong assumption.
In this case, the optimal line set L* depends on the elapsed wait time and is therefore no longer constant. Determining the set is more difficult than in the previous cases. It can be proven that L* has the following shape.
Given are i* ≤ n and an orderly sequence of times 0 ≤ ti* ≤ ... ≤Tl.tl. This means that in time interval Ij= (tj+1,tj] just Lj = {1, ..., j} forms the optimal line set. tj is here the exact point in time t, from which onward the remaining journey time of line j is greater than or equal to the expected remaining costs (including wait time according to t) of the lines Lj-1. In other words, tj is the unique solution for t in 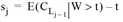 .
.
The optimal strategy is as follows. If the passenger observes an arrival of a line from Lj, after wait time τ ∈ Ij, he will board that line. Other lines he will ignore.
One can show that this strategy reduces the expected remaining costs. As illustrated in the following, it corresponds more with the real behavior of passengers than its abstract definition.
Because the passenger knows the headways of all lines, his knowledge on which available lines are still worth taking, increases the longer he is waiting. Comparable slower lines may still be reasonable options at the beginning of the wait time. There is a time, however, when the evaluation “topples”. At a certain time, the expectancy for the remaining wait time for the faster j-1 lines is less than the difference between their remaining travel time and the remaining travel time of the line j. Exactly as of this time is it no longer worth it to take line j – even if it arrives immediately. The times tj mentioned above are exactly those moments when a line j is no longer included in the optimal line set L* for this reason.
Example
Let us regard the following simple situation of two lines.
|
Line |
Run time |
Headway |
|
1 |
10‘ |
15‘ |
|
2 |
13‘ |
15‘ |
The passenger waits maximum 15 minutes to continue his journey. After t minutes the expected remaining travel time for line 1 is exactly 10 + (15 - t) / 2 minutes. To determine the point of time as of which this expected value is less than the run time of line 2, you resolve 10 + (15 - t) / 2 ≤ 13 according to t which results in t ≥9, thus t2 = 9.
In other words, a vehicle of line 2 can be ignored after 9 minutes, because the three minutes longer run time of line 2 is not made up by the mean remaining wait time for line 1.

